Marshall Davey and Charles Puelz’s paper, which was co-authored by Simone Rossi, Margaret Anne Smith, and David Wells and entitled, Simulating cardiac fluid dynamics in the human heart, has been accepted for publication in PNAS Nexus. (An earlier preprint is available on arXiv.) The study was also performed in collaboration with Greg Sturgeon and Paul Segars at Duke, John Vavalle at UNC School of Medicine, and Charlie Peskin at NYU.

Predictive mathematical models of blood flow in the heart can simulate cardiac physiology, pathophysiology, and dysfunction along with responses to interventions. However, existing models of the heart are limited in their abilities to predict valve performance, use realistic descriptions of tissue biomechanics, or predict the response of the heart to changes in loading conditions. The integrative model of the human heart introduced in this paper aims to address these limitations. It generates pressure-volume loops, valvular pressure-flow relationships, and vortex formation times that are in excellent agreement with clinical and experimental data. The model also captures realistic changes in cardiac output in response to changing loading conditions. Critically, these physiologic aspects emerge inherently from mechanistic interactions within our comprehensive description of cardiac physiology.

This paper advances the state-of-the-art in modeling cardiac fluid-structure interaction.

Congratulations, Marshall, Charles, and the rest of the team!

The paper by group alumnus Aaron Barrett, along with Cole Gruninger, Flagellum pumping efficiency in shear-thinning viscoelastic fluids, has been accepted to appear in Journal of Fluid Mechanics. This study was also done in collaboration with Greg Forest at UNC and with Aaron Fogelson at the University of Utah.

Congratulations, Aaron and Cole!

Cole Gruninger’s paper, with group alumni Aaron Barrett and Fuhui Fang and entitled, Benchmarking the immersed boundary method for viscoelastic flows, has been accepted to appear in Journal of Computational Physics. This study was also done in collaboration with Greg Forest at UNC.

Congratulations, Cole, Aaron, and Fuhui!

Keon Kim’s paper, which is with group alumnus Amneet Bhalla and is entitled, An immersed peridynamics model of fluid-structure interaction accounting for material damage and failure, has been accepted to appear in Journal of Computational Physics.

Congratulations, Keon and Amneet!

The paper by group alumnus Amin Kolahdouz, along with David Wells and Simone Rossi, A sharp interface Lagrangian-Eulerian method for flexible-body fluid-structure interaction, has been accepted to appear in Journal of Computational Physics. This work was also done with our FDA collaborators Kenny Aycock and Brent Craven.

Congratulations, Amin, David, and Simone!

The paper by group alumnus Aaron Barrett, along with Jordan Brown, A model of fluid–structure and biochemical interactions for applications to subclinical leaflet thrombosis, has been accepted to appear in International Journal for Numerical Methods in Biomedical Engineering. This study was also done in collaboration with John Vavalle at UNC, Arash Kheradvar at UC Irvine, and Aaron Fogelson at the University of Utah.

Congratulations, Aaron and Jordan!

David Wells and Ben Vadala-Roth’s paper, which was also written with Mike Lee and is entitled, A nodal immersed finite element-finite difference method, has been accepted to appear in Journal of Computational Physics.

Congratulations, David, Ben, and Mike!

Jordan Brown’s paper, Patient–Specific Immersed Finite Element–Difference Model of Transcatheter Aortic Valve Replacement, has been accepted to appear in Annals of Biomedical Engineering in their Special Issue on Modeling for Advancing Regulatory Science.

Congratulations, Jordan!

Simone Rossi and Laryssa Abdala’s paper, Rule-based definition of muscle bundles in patient-specific models of the left atrium, has been accepted to appear in Frontiers in Physiology.

Congratulations, Simone and Laryssa!

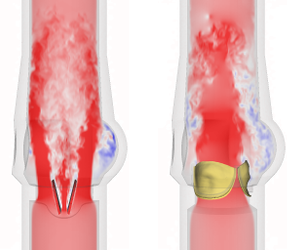
Mike Lee’s paper, On the Lagrangian-Eulerian coupling in the immersed finite element/difference method, has been accepted to appear in Journal of Computational Physics. (A preprint is available on the arXiv.) This paper systematically tests the accuracy of the immersed finite element/difference method (IBFEMethod in IBAMR) using different regularized delta functions and relative mesh densities for several benchmark problems along with our large-scale model of a bioprosthetic heart valve in a pulse duplicator. Our results indicate that kernels satisfying a commonly imposed even–odd condition require higher resolution to achieve similar accuracy as kernels that do not satisfy this condition. We also find that narrower kernels are more robust, in the sense that they yield results that are less sensitive to relative changes in the Eulerian and Lagrangian mesh spacings, and that structural meshes that are substantially coarser than the Cartesian grid can yield high accuracy for shear-dominated cases but not for cases with large normal forces. I think this will be a very useful study for practitioners of the IB method.

Congratulations, Mike!